The Teacher’s Guides cover this in more depth, this is a good introduction that shows how simple the normally complex “concept” of fraction division can be!
Before showing how to use Fraction Bars to divide ¼ by 2/3, lets look at dividing 5/6 by 1/3. Looks tricky, but it can be so easy!
Using the idea of fitting one amount into another, we can see that 1/3 “fits into” 5/6 twice, with 1/6 remaining. By comparing the remaining 1/6 to the divisor 1/3, we see 1/6 is half of the divisor 1/3. So 5/6 divided by 1/3 is 2 and 1/2.
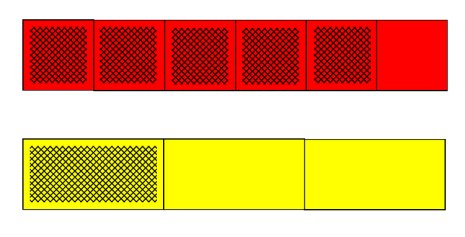
This is similar to the reasoning when dividing one whole number by another. For example, 17 divided by 5 is 3 with a remainder of 2. So the quotient is 3 2/5. In this example, we compare the remainder, 2, to the divisor, 5, and obtain the ratio 2/5.
Now let’s look at ¼ divided by 2/3. Since 2/3 is greater than ¼, it “fits into” ¼ zero times with a remainder of ¼. So we compare the remainder ¼ to the divisor 2/3. To make this comparison, it is convenient to replace the first two bars by bars with parts of the same size. Now if we compare 3 shaded parts to 8 shaded parts, the ratio is 3/8.
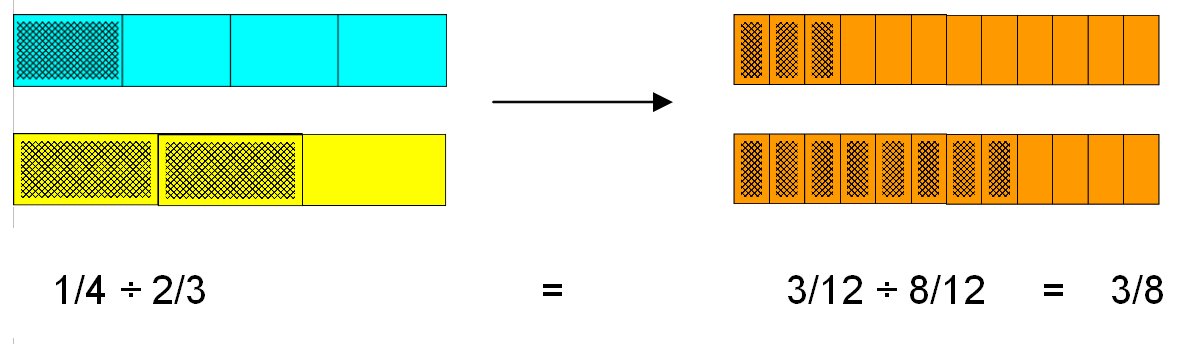
¼ ÷ 2/3 = 3/12 ÷ 8/12 = 3/8
Starting with examples for students where one shaded amount fits into a second shaded amount a whole number of times, students will be able to see that division of fractions is comparing two amounts, just like division of whole numbers. In this way, division of fractions makes sense. An initial example like the one above for 5/6 divided by 1/3 where students can see that 1/3 fits into 5/6 two and one-half times is good. Later bring in the “invert and multiply” rule to show that this method gives the same answers that they can see makes sense with a few simple examples with Fraction Bars. So viewing division as comparing two amounts to see how many times greater one amount is than another, works whether the number being used are whole numbers or fractions. And once we obtain bars with parts of the same size, (i.e. common denominators) finding the quotient of two fractions is just a matter of finding the quotients of whole numbers of part of the same size.
